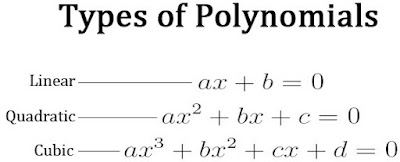polynomials in one variable and its types
Introduction:-
All the expression which consist of variable , coefficient,and constant are called polynomial .
In polynomials the expression like 2x+1 is called a term, each term of polynomial is called a
coefficient, In this therm x is a variable.
In fact, 2,-5,3 etc. are examples of polynomials. The constant polynomials 0 is called the zero polynomials.
Degree of a polynomial is the highest power of the polynomial.
There are three types of polynomials on the bases of term:-
i) Monomial:-
It has only one term.
ii) Binomial:-
It has two terms.
iii) Trinomial:-
It has three terms.
There are three types of polynomials on the bases of degree:-
i) linear polynomial :-
It consist of polynomial with degree 1.
ii) Quadratic polynomial:-
It has polynomial with highest degree 2.
iii) cubic polynomials:-
It consist of polynomial with highest degree 3.
~ zeroes or roots of polynomials refers to there solution.
- A zero of need not be 0 only.
- 0 may be a zero of polynomial.
- Every linear polynomial have only one zero.
- A polynomial can have more then one zero.
~ zeroes of polynomials can be find using factor theorem, reminder theorem, splitting the midterm method, completing the square method etc.